For us to answer this question we need to understand the motion of objects under the action of external forces, in other words mechanics.

    Arguably the most important physicist of our time was Sir Isaac Newton (1643-1727). In 1687 he published his Philosophiae Naturalis Principia Mathematica that set out of mathematical principles governing the behaviour of the Universe. Newton was 23 at the time. The fundamental laws of motion that he formulated combined with calculus are the mathematical tools which we need to understand rocket motion and orbits!

IMAGE - An Artists Impression of Young Newton

Launching XMM

     XMM was launched on an Ariane V rocket. We need powerful rockets to overcome the force of gravity of the Earth. A rocket motor is therefore simply an application of Newtons 2nd Law:

F=ma

     The rocket engines provide a force (or thrust) that is greater than the pull of the earth on the rocket and satellite. For Ariane V there is a main propulsion system called Vulcan which can deliver 1130 kN, two solid state rockets that deliver 5400 kN each for 130s, and a final upper stage motor that provides 29 kN for 1100 s. Ariane has a total launch mass (rocket + fuel + satellite) of 737,000 kg. This mass corresponds to a weight on the ground of mg=7230 kN. (Note the difference between mass and weight - the weight of XMM in orbit vanishes, but its mass is unchanged).

IMAGE - The Ariane Rocket.

Please move your mouse over the image above.

     A quick calculation shows that the total rocket thrust available at launch is 11,930 kN - more than enough to lift the rocket. Most of the thrust, about 90%, is actually provided by the two solid rocket boosters and these burn up after just 130 seconds into the flight and are then jettisoned. There is no point carrying `dead mass' into space.

Rocket thrust and momentum conservation

     So how does a rocket motor generate thrust? The thrust is simply generated by the mass of the fuel that is propelled out of the rocket motor at high velocities, typically up to 4,300 m/s. Remember that the force is given by the rate of change of momentum:

F=ma=dp/dt

     Since the overall momentum of the rocket+exhaust must be conserved, we can see that the momentum generated by the rocket exhaust translates into an equal thrust in the opposite direction that pushes the rocket upward against the pull of gravity.
     Numerically, the thrust of the rocket is given by Thrust = dm/dt * v where dm/dt is the burn rate of fuel and v is the very high exhaust velocity. To illustrate this, take as an example the Vulcan main engine on Ariane V. This engine burns 158,000 kg of fuel over 600 seconds at a more or less constant rate. Taking the exhaust velocity above of 4,300 m/s, you can easily calculate that the thrust from the rocket is close to the number 1130 kN, quoted above for the Vulcan engine.

The Vulcan engine can deliver a thrust of 1130kN and the exhaust velocity can be as much as 4300m/s !

Please place your mouse cursor over the ON switch

Orbits and centrifugal force

     Once XMM had been boosted by Ariane to an altitude which placed it well above the Earth's atmosphere (which absorbs X-rays) it was injected into an orbit. The orbit of XMM is actually highly elongated, but it is easier to understand the properties a simple circular orbit. Consider the simple example of an object whirling around on a piece of string. The string applies a tension force to the ball that keeps it accelerating around the circular path, just like a satellite in orbit.

What happens if you cut the string?

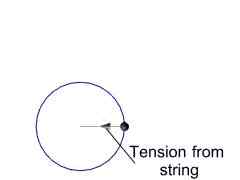
Please place your mouse cursor over the images

     The ball flies off! However, it moves off in a direction at a tangent to its circular path. The direction of the ball is therefore continuously being changed by the tension in the string so that it moves in the circular path and not in a straight line. The tension in the string is therefore analogous to the force of gravitational attraction between the satellite and Earth pulling the satellite in a circular path. The relationship between tension T and the ball's velocity v is given by

T = m * (v²/r)

     where r is the radius. The force acting outwards, which is balanced by the tension in the string (or in the case of a satellite, by the force of gravity) is the centrifugal force.

Please place your mouse cursor over the images

Summary of Terms

• Inertia - The property of things to resist change in motion.
• Mass - The quantity of matter in an object. More specifically, it is the measure of the inertia or sluggishness that an object exhibits in response to any effort made to start it, stop it, deflect it, or change in any way its state of motion.
• Weight - The force due to gravity on an object.
• Force - Any influence that can cause an object to be accelerated, measured in newtons. Large forces may be measured in kilonewtons (kN).
• Newton - The SI unit of force. One newton (symbol N) is the force that will give an object of mass 1kg an acceleration of 1 ms^-1

The End of the FORCE AND MOTION topic.