


The Schwarzschild Radius
The Schwarzschild radius rs defines a sphere around a black hole called the Event Horizon. At the distance of the Schwarzschild radius, the escape velocity (the velocity required to overcome the attraction of gravity) from all points on this Event Horizon is equal to the velocity of light (300,000 km/s). Nothing can travel faster than light and so even light itself is only just able to overcome the gravitational attraction of the Black Hole. Thus, nothing at all will be able to escape from within the Event Horizon, where the attraction is even stronger. (In comparison, the escape velocity from the surface of the Earth is only 11 km/s.)
A particle of mass m
which is moving through the event horizon with
velocity v will have kinetic energy
mv2/2.
It will also have potential energy
GmM/rs due to the
gravitational force of the Black Hole, where M
is the mass of the Black Hole and G is the
Universal Constant of Gravity. The particle
will just be able to leave the Black Hole
(i.e. get to infinity) if its kinetic energy
equals its potential energy; if its kinetic
energy were any less it would come to rest
sooner. So
![]()
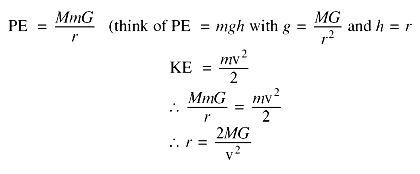
![]()
If we put r = rs = the Schwarzschild Radius, and v = the maximum escape velocity = c
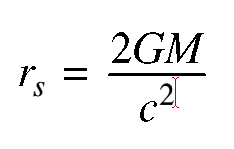
![]()
As an example, the Schwarzschild Radius of a
Black Hole equal in mass to the Sun is 2.5 km.
(This calculation, which treats photons as material particles,
and uses Newton's theory of gravity in place of Einstein's General
Relativity, is somewhat dubious, but it does give the right answer.)

