What is resononce?
Resonance is one of the most important concepts in physics and crops up in a great variety of situations.
The example usually used to demonstrate resonance is the tuning fork. If you put some energy into the prongs of a tuning fork it will vibrate and make a sound at a particular, characteristic frequency. If we take this tuning fork (which is now no longer vibrating) and play a note on a piano which has the same frequency, we notice that energy is transmitted through the air to the fork which now starts to vibrate. The same thing will not happen if we play the next note up on the piano. However, if we play the same named note but at a different octave or any other "harmonic" note, then energy will again be transmitted to the fork. Resonance is sometimes called a "sympathetic vibration" and occurs only when the frequencies of the transmitter and receiver are matched (or bear some simple relationship to each other; i.e. are harmonically related).
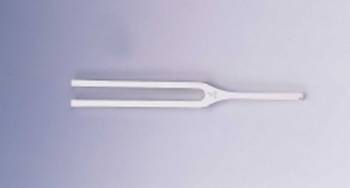
If we take this example one stage further and put our tuning fork in a concert hall in which an entire orchestra are just playing a whole lot of random notes as they tend to when tuning up before the conductor comes on, then we would again find that the tuning fork starts to vibrate. That is to say, from the whole range of sound frequencies present the tuning fork is selective in acquiring energy from that frequency to which it is tuned.
What is the natural frequency of a system
If a system is said to be in a position of stable equilibrium it is kept in place by two opposing and balanced forces. Any displacement from its stable position will cause the forces to be in imbalance and the result will be a restoring force (the magnitude of the imbalance) which attempts to bring the system back to its rest position. If the restoring force is proportional to the displacement then, when the system is released from its displaced position, the system will undergo oscillations at a frequency which is natural for that system. This is its natural (or characteristic) frequency.
What is simple harmonic motion?
The system above was displaced by putting (potential) energy into it. When the system is "let go" provided there is no damping it will execute a cycle whereby it returns to its original displaced position and the cycle will then start again. Without damping it thus continues to oscillate for ever. This is called Simple Harmonic Motion (SHM). Its motion is periodic, or cyclic. The natural frequency of a system is therefore the frequency of the SHM of that system. During this cycle energy is exchanged from potential energy into the kinetic energy of motion and then back again. The period is the time for a single cycle to be executed (and has dimensions of time, T), and the frequency of the oscillation is the number of cycles per unit time (and has dimensions of T-1 ). Hence there is a reciprocal relationship between time and frequency.
The time for a cycle must have to do with the distance travelled by the displaced component and the speed with which it travels in executing that cycle. Time is distance divided by speed. We can use this simple idea to get some idea of what determines the period of a system by considering a few simple examples.
Consider a pendulum comprising a mass suspended from a pivot point by a massless string of length l. We displace the system by an angle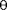 
and let go.
The swinging motion of a pendulum is an example of simple harmonic motion. The Period of the swing does not depend on the mass on the end of the string, only the length of the string and how strong gravity is.
Please move mouse over image
The distance that the mass has to travel in a cycle can be represented by the product l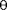 . The force along that direction is a component of the weight of the mass which is represented by mg.sin 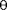which, for small 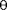approximates to mg 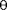. Hence the acceleration , and consequently the speed, can be represented by g 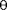. Thus the period must be represented in some way by the quotient of the two name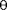ly l /g or simply l/g.
Here, by displacing the mass, the mass is raised and therefore energy is stored as gravitational potential energy.
Let us consider a different system, the spring.
The spring is displaced from its rest position by a distance x and let go. Here the distance travelled per cycle is to do with x; the force is to do with kx, where k is the stiffness of the spring and hence the speed is to do with kx/m. Taking these together, we can represent the period in some way by x/(kx/m) or simply m/k.
Here the displacement stores potential energy into the spring via the binding forces between the atoms in the metal.
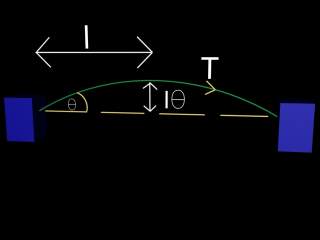
One final example which combines the principles of both the above is the stretched string. An application of this is the string on a stringed instrument such as a piano or violin. Let the string of length 2l be secured at each end and subjected to some tension T. Let the string be displaced by some angle .
PLease move mouse over image
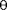Here the distance to travel is associated with l , the force with T , and hence the speed with T 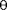/m where m is the mass of the string. We therefore expect the period to somehow be represented by l 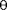/(T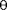 /m) or ml/T.
If we adopted a more rigorous approach we would be able to determine the actual mathematical functions for the periods and thus show that their associated natural frequencies are respectively
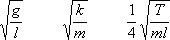
We can see from this approach that the natural frequency of a system is associated with properties inherent to the materials used and with characteristics of the assembled system (the structure) and we can see the kinds of parameters which might be involved in any given system. For example in the case of a tuning fork it would seem that k, m and l might be involved in defining its natural frequency. And for more complicated structures such as bridges we may not be too surprised to see some of the other parameters involved as well, depending on whether the bridges are of the cable type working under tension or of the solid type working under both tension and compression.
