


![]() What have tuning forks got to do with spacecraft?
What have tuning forks got to do with spacecraft?
![]()
![]()
We have tended to talk about tuning forks because they are a very simple structure. We could equally have talked about a bell, such as an old fashioned alarm bell or a church bell. These are more substantial structures but they are similar to a tuning fork in that they make a characteristic note. The note is not so ‘pure’ as that of a tuning fork but none the less you could still ‘hum’ it. When we say it is not so pure we mean that it supports not just one frequency but a number of frequencies. For the same reason different musical instruments playing the same note still sound different because besides the strong, fundamental frequency they contain different selections of other, weaker frequencies.
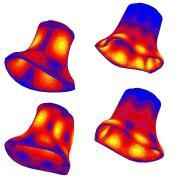
This image shows analysis of the vibrational frequencies of vibrating bells. The lighter reqions show regions of greater vibration.
One can almost imagine being able to make a spacecraft structure out of bells and tuning forks. This serves simply to show that any structure will have its characteristic frequency (its fundamental frequency) together with a collection of other natural frequencies. Each frequency will have its associated Q factor depending on how lossy the structure is. For example a bolted structure will be more lossy than a welded structure and similarly any fabricated structure has more inherent damping than a structure machined out of solid.
Having made our ‘tuned’ spacecraft we now put it on a rocket and launch it, that is to say we subject it to an environment that contains a whole lot of different frequencies of large amplitudes, or in other words high level noise. The payload is subjected to the quasi-steady accelerations that are necessary to increase the velocity of the rocket and these will not get amplified (by definition they do not have an associated frequency). But of those other accelerations that we discussed earlier, some will occur at the natural frequencies of the payload and will be selected and amplified by a factor determined by the Q factor at each of the frequencies.
Just to put a few numbers to these accelerations. We saw earlier that the quasi-steady accelerations may be of order 5g or so. The input g values associated with some of the high intensity noise vibrations could be as high as 5 to 10g and, given a Q factor of say 5, accelerations in excess of 25g could well be experienced by the structure. That is to say, the structure has to support the equivalent of at least 25 times its own weight.
This can have two important effects. If either the inputs are too high or the damping is too low then the induced forces in the payload can be so high that the structure simply fractures or falls apart. But this structure is still attached to the rocket and can now feed the amplified forces back into the rocket and can cause similar problems for the rocket. This is referred to as ‘the tail is wagging the dog’.
How can resonance effects be avoided?
First let us address the tail wagging the dog. Rockets are long structures and therefore tend to have low resonance frequencies (recall that l appears in the denominator of the frequency formulae we showed earlier), certainly lower, in general, than those of payloads (notwithstanding telescope type payloads). Usually the approach is simply for the project to require the payload engineers to design a structure with no resonances below a given figure, usually about 80 to 100 Hz.
The vibration spectrum generated by a given rocket is fairly well defined. Again in general terms, most of the noise is generated in the frequency range up to about 1000 Hz. At higher frequencies the levels of noise are usually much less.
We have seen from our discussion that there are two principal ways to avoid a resonance effect at a particular frequency; shift the natural frequency to some other frequency or introduce some damping to reduce the Q factor.
The former is usually achieved by designing the natural frequency to be at higher frequencies where the input accelerations are usually lower. Again, reference to the frequency formula show that this can be done by reducing mass (or redistributing the mass), reducing the length of unsupported structures or increasing the stiffness of materials. Note that these are not necessarily independent variables since the density is involved in a number of them.
Designing for a certain damping is very complex. Computer modelling of structures is sophisticated and reliable in so far as it can accurately predict what the resonance frequencies are, but it does not predict the damping (since so much depends on how the structure is actually manufactured and put together). Q factors are therefore calculated within the model on the basis of some assumed level of damping inputted to the model and which is itself based on experience.
If neither of the above can be implemented then the bullet has to be bitten and the system designed to be strong enough to withstand the forces imposed.
A combination of computer modelling and vibration testing are generally very effective in ensuring that payloads, which have probably had much time and thought put into them, safely survive the launch.. In the old days a flight spare payload was often built as a back-up in the event of failure. These days such luxuries are too expensive so it has to work first time!
What happens when resonance effects aren't avoided?
Needless to say the results can be very dramatic. Witnessing such dramatic events is rare, certainly in the space business. But just look at the effects of resonance on the Tacoma Narrows suspension bridge in the United States where a resonance was excited by high winds. Fortunately these days not only can good computer models be made but representative scale models can be built and tested in wind tunnels. Having said that though, there were still problems with the millennium footbridge built over the Thames!



