"The universe is expanding." You hear this and read this all the time in astronomy circles and books; normally it is followed by something like, "All the galaxies are getting farther apart," and a plot called a Hubble diagram. Just about every graduate student in astronomy has (re-)done the mathematics of General Relativity which describe the expansion, and there is no dispute among astronomers about how to calculate it. But what is happening, and why, on an intuitive level is much fuzzier. I found myself looking into the matter after meeting a particularly confusing presentation. The result, with all the mathematics, was published in the Observatory, vol. 124, pp. 173-189, in June 2004 and on the astro-ph eprint server. What follows here is a short summary without the mathematics.
Modern cosmology, the part of astronomy which deals with the universe as a whole, was created and continues to be studied in the context of General Relativity. This is in a way unfortunate, for GR (as it is affectionately known) uses a very different set of ideas and processes than its predecessor, Newtonian mechanics. We are comfortable with objects moving in Euclidean three-dimensional space as time progresses, the Newtonian picture; we are not so comfortable with objects describing geodesics in four-dimensional pseudo-Riemannian space-time. (At least everyone I've met is more comfortable with Newtonian ideas, with the possible exceptions of Roger Penrose and Stephen Hawking; but I've met them only briefly and can't say I'm familiar with either.)
In GR, the three-dimensional space of the cosmological universe is generally pictured as a sort of expanding rubber sheet, with the galaxies (and all appertaining thereunto) fixed on it, expanding along with it. In this picture galaxies don't seem to be moving at all; it's just that space is expanding, forcing them apart. This is the description of, for instance, Odenwald and Fienberg in Sky & Telescope, vol. 85, p. 31 (1993).
But if we look only at nearby galaxies, they're normally depicted in the Newtonian way: moving (at so many kilometers per second) through space away from us. Putting the two modes of thinking together, perhaps this means that (what in GR language is) space itself exerts (what a Newtonian would call) a force on each galaxy, pushing it away from all the others. If this is true it means, for instance, that a massless test particle (recognized by both relativists and Newtonians) held at arm's length and released would move away from you.
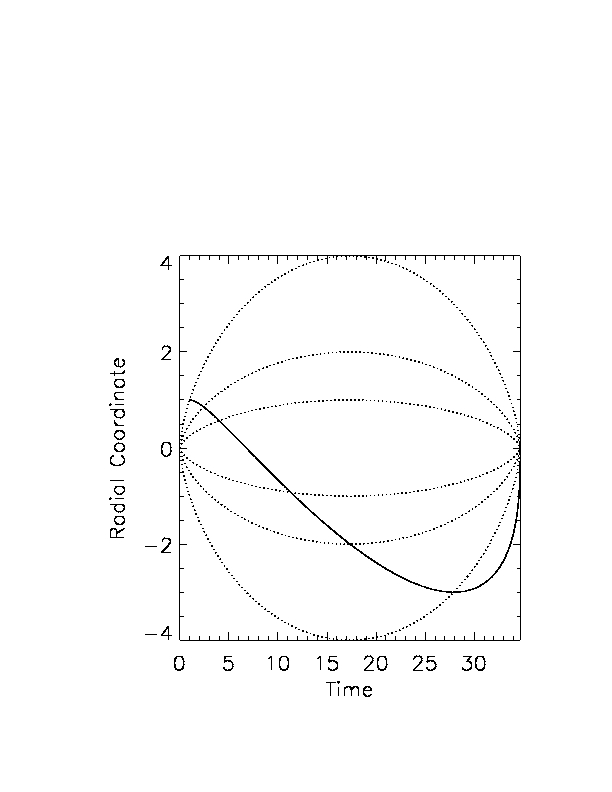
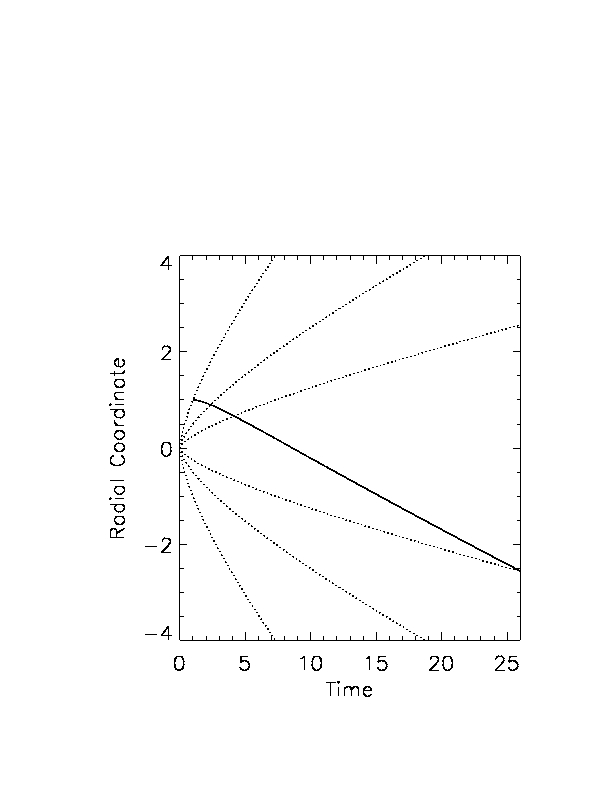
That doesn't happen. Working through the equations gives the results shown below. In the left-hand one, the universe as a whole (the dotted lines track various galaxies) expands, reaches a maximum, and contracts. (This does not describe the universe we're in, but it's allowed by the cosmological equations). The test particle starts by moving toward you ("you" are at the radial coordinate of zero) as soon as it's released. In the right-hand plot, the universe expands indefinitely; still, the test particle comes home, before going out the other side.
 |
 |
Neither does space exert a sort of viscous force, like honey or water. On the left it's pretty clear that its motion is always separate from that of the universe in general. On the right it appears that it eventually joins the flow, but examining the mathematics in detail it's clear that it never actually does.
So the expansion of the universe is not due to some mysterious force out of General Relativity. In fact one can think of it in a strictly Newtonian way, with galaxies having some initial velocity and slowing down due to their mutual gravitational attraction. You have to be careful about applying Newtonian physics to cosmology, but it has been investigated and (within its limitations) is quite legitimate.
But descriptions of the cosmological redshift almost always use the picture of the expanding rubber sheet, and are generally careful to say it's not due to relative motion, not a Doppler effect. This time the light is conceived as sort of painted on the rubber, so that it expands in step with the "universe". This idea even gives the right mathematical form for the redshift equation.
But there are reasons to be uneasy with this picture. Atoms are held together by electromagnetic forces, so they should expand along with the universe, and we should never see a cosmological redshift (the atoms in our measuring devices should expand exactly as much as the wavelengths of light rays). At the very least, comparing radiation from different parts of the universe should be extremely complicated--and it isn't. In addition, the equation of cosmological redshift can be derived assuming that it does come from relative motion, in a particular way. The expanding rubber sheet is not an analogy, or a picture, that you can push very far.
What is the answer? The best thing I've come up with is a diagram in two dimensions: cosmic time (which, because of the symmetry of an isotropic, homogeneous universe is agreed upon by all observers in the Hubble flow) and some spatial direction in which a light ray is moving. Two points on the light ray, say the beginning and the end of one wavelength (the neighboring points where the electric field vectors are zero), are traced as they propagate. Draw the quadrilateral: one side is the wavelength at one time; the opposite side, the wavelength at a later side; the remaining sides, the paths of the two endpoints through space and time.
If you can draw this quadrilateral on a flat piece of paper, then this section of spacetime is called "flat", and there is no cosmological redshift. You can calculate with Special Relativity (SR is much easier to use than GR). A genius by the name of Milne built a cosmology out of something like this. Unfortunately, it requires that there be negligible mass in the universe, and doesn't seem to correspond to ours.
If the universe is an expanding one as described by GR, then the side of the quadrilateral made up of the wavelength at the later time will be longer than the side made up of the wavelength at the earlier time. You won't be able to draw it on a flat piece of paper; you'll need something curved, along the lines of a potato chip.
The answer, then, is that the cosmological redshift comes because light propagates (a fancy word for "moves") through a part of the universe which, taken as a section in one space direction and time, has a curvature. It can't be stopped at a single time and considered to be painted on space (stopped light, in a vacuum at least, disappears); it has to move. And the time-space section has to have a curve. (Two, or even three, spatial dimensions taken together can be flat. The important thing is that the direction the light goes in, taken together with cosmic time, must be curved.)
These explanations may seem to make things more complicated, but they should make at least some things less mysterious. There is no strange, relativistic cosmic force pushing things apart. You can treat reasonably small sections of the universe with Newtonian physics, as long as things are not moving relative to each other at a significant fraction of the speed of light (in which case you'll need SR), and as long as you aren't dealing with really strong gravitational fields (like those near neutron stars or black holes, which need a local application of GR).
And the effect of the expanding universe on smaller things, like galaxies, the Solar System, the Earth and you, is--zero. It's like an ant crawling on one rock on an immense mountain: the slope of the mountain as a whole is irrelevant.
Return to: