FORCES ON MOVING CHARGES - cont'd

What is the effect of the force?

     What effect the force has on the electron very much depends on the circumstances of the electron. There are three situations that we are going to consider; the electron in the atom, the electron in the metal, and the free electron.

ANIMATION - Electrons bound to a nucleus, electrons in a metal producing a sea of electrons and a free electron

What is the effect of the Lorentz force on the electron in the atom?

     The negatively charged electron is bound to the positively charged nucleus by coulombic forces and remains in this stable configuration.

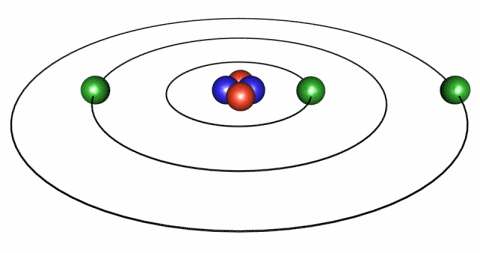
IMAGE - The classical representation of the atom.

Classically, electrons follow discreet orbits around the nucleus analagous to the planets in our Solar System.

     There are different ways in which we can view this scenario. One view is the "classical" view in which we visualise the electron as orbiting the nucleus so that coulombic forces are balanced by centripetal forces. However, from a classical standpoint since such an electron is therefore being accelerated it must therefore radiate, lose energy and spiral into the nucleus. The implication of this was that the atom could therefore not be a stable system.

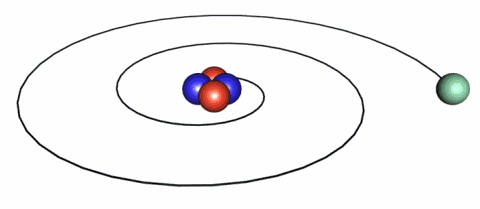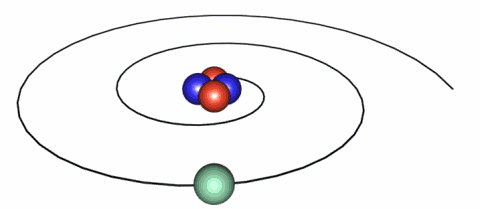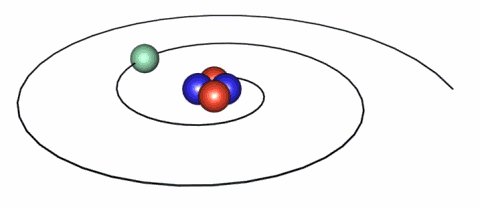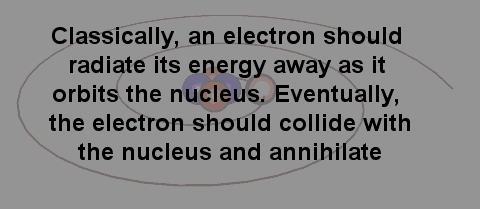
IMAGE - The classical picture of an electron.

A problem with the classical picture is that the accelerating electrons will radiate energy away and therefore spiral into the nucleus.

     The model was adapted to preclude the electron from continuously radiating in this way; that is, classical physics was deemed not to apply in this respect on such small scales as this. In addition it was postulated that the electron could only occupy certain, specified orbits whose energies were quantised and that energy was either absorbed or emitted as a result of electronic transitions between these orbits. This semi-classical, quantum model, which was known as the Bohr Theory of the atom, was later to be replaced by the wave mechanical model of the atom in which the electron was represented, not by a classical particle, but by a probability wave..

IMAGE - The quantum picture of the atom.

The quantum picture represents electrons (in fact all particles) as probability waves. Therefore, an electron is nowhere but everywhere at the same time!!!!

     However, for our purposes it is still useful to envisage the electron orbiting the nucleus in a stable orbit and able to do so without radiating.

     If we were to consider such a circulating electron in a magnetic field as is shown in the diagram and apply the Lorentz force equation (taking care to get the directions right), we see that a couple or torque is experienced by the electron in its orbit.

IMAGE - A magnetic dipole in a magnetic field.

The dipole will experience a torque which will reorientate itself in the opposite direction to the magnetic field.

     In our example, the couple is turning the atom in such a direction as to maximise the angle between the field and the plane of the orbit. As this happens the couple decreases in magnitude until the situation is reached where the orbital plane of the electron is perpendicular to the field and the couple is zero (the Lorentz forces all point to the centre of the orbit).

     In this state the torque is zero and there is no net turning force on the electron. The electron is therefore in its lowest energy state as regards its orientation with the magnetic field.

IMAGE - A magnetic dipole reorientated in a magnetic field.

     However we are in the quantum domain and, in a similar way to that above in which the orbiting states of the electron had to be quantised, so too are the "allowed" orientations of the (electron) orbit with the magnetic field in this example. These different orientations have different associated energies. These manifest themselves when we look at spectral lines of atoms when these atoms are placed in a magnetic field. This is called the Zeeman Effect which causes the lines to "split".

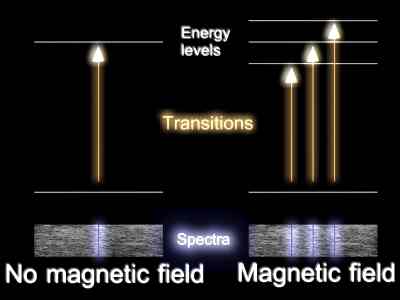
IMAGE - The Zeeman effect

Due to quantum effects, the atom has discreet energy levels. When placed in a strong magnetic field, these energy levels split further resulting in spectra as shown above.

What is meant by the magnetic dipole moment of the system?

     In our example the circulating electron represents a current, albeit very small. The direction of the current is opposite to the direction of motion of the electron. (Recall, in an electric circuit, conventional current goes from the positive terminal to the negative terminal, whereas the (negatively charged) electron is attracted to the positive terminal). The current has an associated (dipole) magnetic field and, if placed in a magnetic field, experiences a couple on the current to turn it such that its magnetic field lies in the opposite direction to the applied field (see below).

     [It may be helpful here to think of two bar magnets and their respective fields. If placed end to end the minimum energy situation is when the north pole of one is facing the south pole of the other. Or, if placed side by side when the magnets are facing opposite directions. In each case the respective field lines of the magnets in the vicinity of the interaction regions are in opposite directions.]

IMAGE - Two bar magnets and their magnetic fields, one on top of the other and two side by side.

     Because of this couple (forces acting at a distance) we can talk of the current loop as having a moment; in this case a magnetic dipole moment. The magnetic moment is a vector and has a direction the same as that of the magnetic field it produces inside the current loop (right-hand rule).

     The position of minimum energy as described above is therefore with the magnetic moment in a direction anti-parallel with the applied field. Since the respective fields are now in opposite directions, the net effect is a reduction in the overall magnetic field. This property is called diamagnetism.

     It is the resultant sum of the different magnetic moments of different elements that gives rise to macro magnetism as we know it in solids and which account for the properties of diamagnetism, paramagnetism and ferromagnetism.

     The magnetic moment m is described mathematically as

     where I is the current and A is the area enclosed by the current loop.

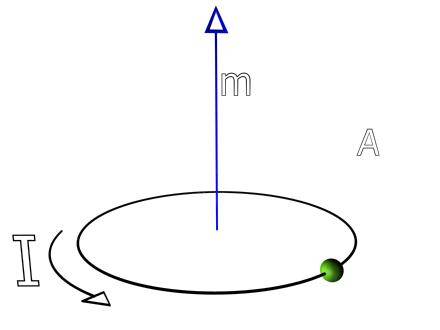
IMAGE - The magnetic dipole.

The cirulating current gives rise to a magnetic dipole field. The magnetic dipole is defined as m=IA.

     Given this we can now express in mathematical terms what we have talked about above.

     The torque tm experienced by the loop in an applied magnetic field B is

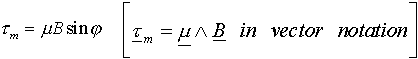
     where j is the angle between the magnetic moment and the applied field

    We can also write down an expression for the magnetic potential energy of the dipole in the field, this being

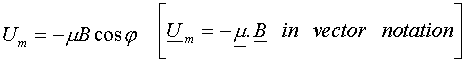
Is there an equivalent electric dipole moment?

     We saw under the topic Forces, E Fields & B Fields that the field configurations of electric dipoles and magnetic dipoles are of an identical form. We can therefore expect that when an electric dipole is placed in an electric field, torques are also experienced so we can talk about an electric dipole moment. Since the dipole will orient itself in order to reduce the torque we can also talk about the potential energy of the system.

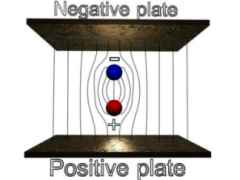
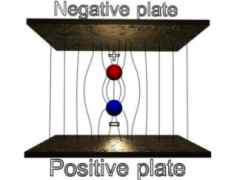
IMAGE - An unstable and a stable magnetic dipole in an external magnetic field.

A magnetic dipole will be stable if its magnetic field lines are running in the opposite direction to the external field.

     Not surprisingly the mathematical expressions are equivalent to their magnetic counterparts.

     Defining the electric dipole moment as :

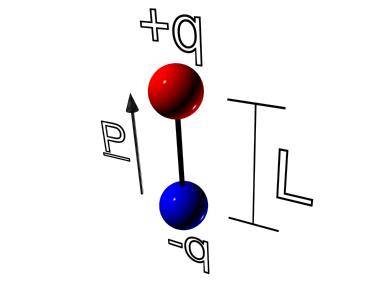
IMAGE - The electric dipole.

     where l is the separation of the positive and negative charge q, we can write the torque in an electric field E as :

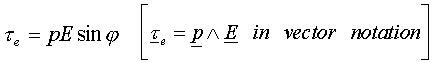
     and the potential energy as :

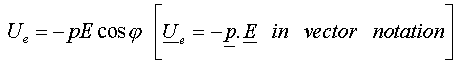
     If we place an atom (or molecule) in an electric field, because the coulombic forces are in different directions for the different signs of the charge, the charges tend to separate and become polarised even though the atom is overall neutral. This induced asymmetric distribution charge can have an associated electric dipole moment. Because we are on the atomic level there are only certain orientations that the electric dipole moment can have with the applied electric field and since they each represent a different energy then it follows that the associated energy states are quantised. This becomes manifest when we observe the spectral lines of atoms when a gas is placed in an electric field. This is known as Stark Effect which results in the "splitting" of the lines.

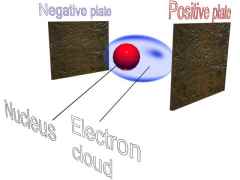
IMAGE - A hydrogen atom in a magnetic field.

The hydrogen atom in the presence of a magnetic field is polarised. The electron cloud is attracted towards the positive plate and the nucleus is attracted towards the negative plate.