


![]() FORCES ON MOVING CHARGES - cont'd
FORCES ON MOVING CHARGES - cont'd
![]()
What is the effect of the Lorentz force on the electron in a metal?
The electrons in a metal which are responsible for it being a metal are electrons which are free in the sense that they are not attached to the atoms in the metal but are not free in the sense that they are constrained to move in the metal.
If we now cause these conducting electrons to move (that is to say, cause a current to flow in a thin wire), and then place the wire in a magnetic field, the moving electrons experience a force but cannot move under the influence of the force because they are constrained by the wire. It is therefore the wire itself that experiences the force. The magnitude of this force is the sum of the Lorentz forces on each of the electrons in the wire. If we consider a length L of the wire that contains N electrons which are moving with an average drift velocity v, then the total force is:
![]()
Where e is the electronic charge.
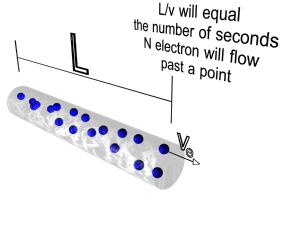
IMAGE - The force on a current carrying wire.
A wire of length L has a total number of electrons N. The value L/v will equal the number of seconds it takes for N electrons to pass a point on the wire. Therefore, the current is equal to Nv/L.
But the current I is the total charge passing a point in unit time and can be expressed as:
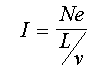
Which gives a total force of:
![]()
If we now use another, straight. parallel wire to establish the magnetic field in which our wire above is placed we see that if the currents in the two wires flow in the same direction there is an attractive force between the wires, but if the current directions are opposite the force is repulsive. Because such forces can be absolutely measured, it was this effect (i.e. the force per unit length of wire) that was used to define the ampere in the SI system of units.
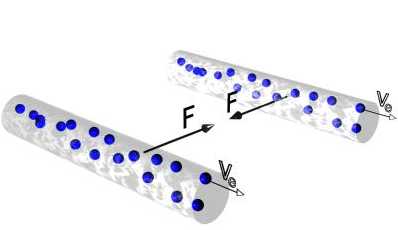
IMAGE - The attraction of two current carrying wires.
If the currents are travelling in the same direction, there will be a mutual attraction. This is how the SI unit Ampere is defined.
If we now form the two wires into a circular loop, it follows that there is a force on the loop to make the loop smaller. The loop has a magnetic field associated with it and therefore a magnetic moment. Hence when we place that current carrying loop in another magnetic field it experiences a torque in just the same way as we discussed previously.
This is the electric coil for which there are applications in our everyday lives which are almost too numerous to count.
![]()
What is the Hall effect?
If we allow our single straight wire that we talked about earlier to have some width, then this allows a (transverse) direction perpendicular to the current flow for the electrons to drift to when we place the device in a magnetic field. Since the circuit in this transverse direction is not complete there is a build up of charge and hence a steady voltage (the Hall voltage) is established which prevents any further drifting in this direction. This is known as the Hall Effect. The Hall voltage can be detected and measured.
IMAGE - The Hall effect.
In this diagram J is the current, B the magnetic field and F is the force. The electrons feel a force upwards which leads to the charge being separated along the wire.
There are many applications of the Hall effect . On XMM Hall devices are used as monitors to detect that the aperture door is either fully open or fully closed. This is accomplished by placing a small permanent magnet on the door arm such that either in the fully closed or fully opened position the magnet is in the proximity of one of two Hall devices. A circuit which checks whether the Hall voltage is above or below a given threshold thus detects the presence of the magnet and hence informs us as to where the door arm is.

