FORCES, E FIELDS & B FIELDS - cont'd

How are forces and field strengths related?

    Fields have to act on something to provide a force. In terms of the gravitational field and the electric field these "somethings" are the mass and the charge respectively. [Here the mass is the gravitational mass. Physicists are still attempting to find any difference between gravitational mass and inertial mass (discussed earlier) but as yet none has been found.]

    Hence :

    where g is the gravitational field strength and E is the electric field strength.

    It is important to note the fact that m can only be positive but q can be either positive or negative. For example the proton and the electron have the same charge magnitude but the proton is positively charged and the electron is negatively charged.

    There are particles called positrons (one of the family of the so called anti-matter) which are just like electrons but have a positive charge. Physicists have not found particles with negative mass though there is no a priori reason as to why they should not exist.

    An electric field therefore produces a negative force on a negatively charged particle which is simply a force in the opposite direction to the field and to that produced by the field on a positively charged particle (recall force is a vector quantity). Hence, if a gas in which the atoms are ionised (i.e. the outer electron has been freed from the electrically neutral atom leaving a positively charged atom behind called an ion) is placed in an electric field, the electrons move one way and the ions move the other.

    So we can see that masses are gravitational type things and charges are electric type things.

What produces the Fields?

    We are familiar with Newtons Law of gravity and with Coulombs Law of electrostatics. They describe the forces between pairs of masses and pairs of charges and are respectively

    Again we note that gravitational forces can only be attractive whilst coulobic forces can be repulsive as well as attractive.

    Comparing these with the two equations above we can see that :

    Hence gravitational fields are due to masses and electric fields are due to charges.

But we also have magnetic fields, so what do these act on and what produces them?

    The force produced by a magnetic field, the so called Lorentz force, is given by

    This equation should really be in its vector form because we would then see that a force is only produced if there is a component of the velocity (v) which is at right angles to the field (of magnitude B) and the force itself is then at right angles to the plane containing the velocity and the field. A force perpendicular to a velocity results in circular motion. We can further see that, because both v and q can have a sign associated with them, the direction of the circular motion can be different.

IMAGE - An animation of a moving charged particle in a magnetic field.

Please move your cursor over this image.

The force is always perpendicular to both the direction and the field, with the direction of a positively charged particle determined by the Fleming's Left-Hand Rule. Since the lorentz force can carry either sign depending on the charge, electrons will move clockwise in the magnetic field described above.

    We can see from this that what magnetic fields act on is (qv), that is, a moving charge. And, by inference from the discussion above, magnetic fields themselves must be produced by moving charges. Hence there is no need to introduce any third agent equivalent to the mass or the charge (such as a magnetic pole); we already have the electrostatic charge and all we need is for it to be in motion

    But a moving charge is a current and it is well known that currents generate magnetic fields.

But what about the field associated with a bar magnet?

    Good question. We will return to this later, but essentially the "currents" are on the very small scale and are associated with the electrons circulating the atoms.
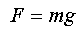
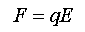
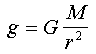
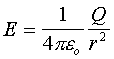
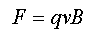