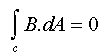FORCES, E FIELDS & B FIELDS - cont'd

How can a field be represented?

    A field is three dimensional and since the field strength at any point has a magnitude and direction it can be described by a vector. Therefore one way of representing and investigating the field is by mathematics using vector analysis. This is not always easily accessible and it can be difficult to get a picture of what is going on.

    An alternative method is to make a two dimensional representation using lines of force. Often the situations being considered have some axis of symmetry so it is quite easy to visualise the third dimension. A line of force simply delineates the path taken by a test particle placed in the field . In the case of gravitation the test particle is a mass and for an electric field a positive charge (the sign of the charge is simply an arbitrary selection). Test particles are however fictitious because they have the properties of the agent itself but have no field lines associated with them themselves. Hence they do not affect the field into which they are placed; they are used simply to sense the direction and magnitude of the field.

    There are certain rules for this representation;

    
• lines can only start or end on the agent (e.g. mass or charge) with which the field is associated or at infinity (they cannot stop in mid space)
      
• lines cannot cross or join up
      
• lines must generally adopt positions of maximum separation consistent with the symmetry of the configuration
      
• the number of lines chosen for each agent is arbitrary except they must be consistently proportional to the magnitude of the agent (e.g. a charge of double the magnitude has twice the number of lines associated with it)
      
• the direction of the line is determined by the direction of the force on the test agent.

    The rules sound rather complicated but are easy to apply especially if we allow some artistic licence in that we cannot draw lines going to infinity (though we can imagine them going to great distances).

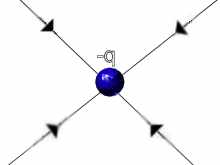
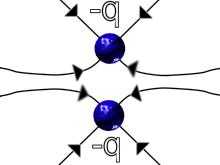
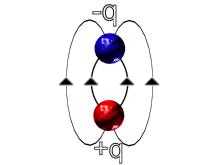
    Here are four examples using positive and negative charges to represent four electric fields.

(a)

(b)

(c)

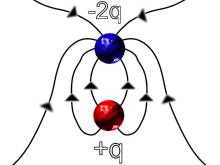
(d)

IMAGE - Four examples of electric fields.

Please see the following text for a detailed explanation.

For an illustration of forces in electric fields which use JAVA please click here

What can we learn from this representation?

    Surprisingly even with this simple model we can learn a great deal. Here are some of the things that these four representations show;

• in (a), (b) and (d) there are lines all the way to infinity; these forces are long range
  
• in (a) and (d) there are the same number of lines going to infinity
  
• in (b) there are twice as many lines going to infinity as in (a)
  
• in (c) there are no lines going to infinity
  
• (d) would look the same as (a) at large distances (large compared with the separation of charges in (d)),
  
• (a) and (b) could represent gravitational fields if we replaced the negative charge with a positive mass
  
• (c) and (d) could not represent a gravitational field because we do not have such things as negative masses
  
• the electric field configuration in (c) looks rather like that of a magnetic field; in each case it is called a dipole field
  

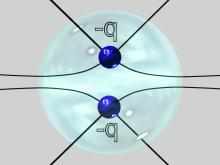
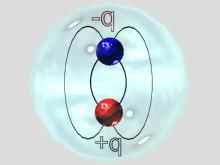
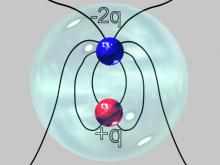
    Hence if we were to surround each of the configurations with a closed surface and count the net number of lines crossing the surface the answers would be

0 for (c)
4 for (a), and (d)
8 for (b)

     Since we have drawn 4 lines per unit charge we see that:

• the surface for (c) encloses zero net charge (+q plus -q equals 0)
  
• the surface for (a) and (d) encloses one net charge
  
• the surface for (b) encloses two net charges
  

(a)

(b)

(c)

(d)

IMAGE - A demonstration of Gauss' Law for electrostatics using the four examples

Gauss' Law is a very important and versatile tool used by physicists. By enclosing charges and applying Maxwell's Equations, very complex electrostatic systems can be solved

    Although what follows is really beyond the scope of the present topic at this level, the next step is an easy one to take and it does tell us about some very important laws in physics. What we have just done is to essentially demonstrate Gauss' Law for electrostatics. The law is:

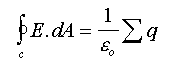
    Where the integral sign shows we are adding or summing something over a closed surface; the something is E.dA where E is the field strength (number of lines per unit area) and dA is the little bit of area; hence the something we are summing is the number of lines. Thus the right hand side of the equation must also be the number of lines and hence 1/₀ is the absolute number of lines that nature associates with a unit charge. See if you can show this for yourself. Click here for the solution. The sign tells us we should perform the algebraic sum on the charges because of their different signs. ₀ is the permittivity of free space, the value of which is about 8.8x10^-12 Fm^-1

    Hence 1/₀ (which is the number of lines which we should have drawn for each charge if we were to accurately represent nature) is about 1.1x10¹¹ which is a very great number of lines to have to draw.

    Similarly we can write down two more of Gauss's laws.

    For gravitation we have:

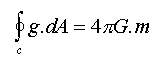
    Remember that m is always positive. We see from this that the number of lines associated with unit mass is 4G. Since G=6.7 x 10^-11 Nm²kg^-2 we see that the number of lines is far less than one line which is impossible to draw.

    And for magnetism we have: