


![]() FORCES ON MOVING CHARGES - cont'd
FORCES ON MOVING CHARGES - cont'd
![]()
![]()
FORCES, E FIELDS & B FIELDS - cont'd
![]()
What is significant about magnetic fields?
The significance lies in the law we have just described which states that if we construct any closed surface in any region in which there is a magnetic field then the net number of lines crossing that surface is zero. That is to say, for every field line coming out of the surface there is a line going back. We say that magnetic field lines are always closed (they never go to infinity). This is different to gravitational and electric lines of force. An example of closed field lines is the dipole field shown as figure (c) in the last section.
Before the unification of the laws of electricity and the laws of magnetism, the concept of positive and negative magnetic poles was adopted in analogy to charges, and indeed was a very useful tool in explaining ideas and observations in magnetism. Hence our familiar dipole field associated with a bar magnet can be described by (c) if we simply replace the +/- charges with +/- poles.

IMAGE - A model of an electric dipole
Electric fields lines of an electric dipole go from the positive to the negative charge
But, if we take a bar magnet and cut it in half we find we have two smaller bar magnets (rather than two isolated magnetic poles). In fact it would appear that magnetic poles always come in dipole pairs and simply do not exist naturally as monopoles. However this has not stopped physicists looking for isolated poles and indeed one of the interesting, unsolved questions in physics is whether monoples actually exist.
![]()
Magnetic field and circulating currents?
Returning to the equation for the Lorentz force:
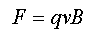
Where qv is the equivalent of our "magnetic" particle.
If we take a charge and move it under the influence of a central force it will move in a circle and will represent a circulating charge which is a current. As Oersted showed in 1820, currents have associated magnetic fields and that of a current loop looks very like a dipole field. That is to say that our "magnetic" particle has its own dipole field (rather than the radial field associated with a charge or a mass).

IMAGE - Model of a magnetic dipole
The circulating current acts as a bar magnet and as a consequence the magnetic field lines are similar to those of a bar magnet
![]()
Are there any similarities between E-fields and B-fields?
From our discussion we see that in the case of the dipole electric field and the dipole magnetic field, the field configurations look very similar. We can therefore expect some similar properties when such dipoles are placed in their applied electric and magnetic fields respectively which can be described by similar equations. We will deal with this under the topic Forces on Moving Charges.
![]()
What is the significance of all of this?
There are two very significant things resulting from this discussion to take on board.
The first is that when we talk about the interaction of moving charged particles with a magnetic field we are actually talking about the interaction between systems of charged particles, and the universe is full of charged particles in motion.
The second thing of significance is that a charged particle moving in a magnetic field experiences a force and is therefore accelerated. An accelerated charged particle produces electromagnetic radiation; in this sense a link is forged between matter and radiation. Indeed the two equations describing Gauss's laws of electricity and magnetism are the first two of the four equations which form Maxwell's equations. Maxwell solved these equations and was able to demonstrate that changing magnetic and electric fields propagate through space as electromagnetic radiation at the speed of light. And of course such changing field are the result of accelerating charges.
Furthermore Maxwell showed the relationship between three fundamental constants of physics:
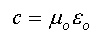
where c is the velocity of light (3.0x 108 ms-1)
and m0 is the permeability of free space (8.9x10-12 Fm-1 )
Had we persisted with our idea of monopoles 1/m0 would have been the number of magnetic field lines associated with a unit monopole.

