


GRAVITY

This image, taken by the Hubble Space Telescope, shows light from a distant galaxy bending as it passes through the cluster, dividing the galaxy into five separate images. The cluster has distorted the shape of the galaxy from a spiral shape to a more arc-shaped. Astronomers are certain the blue-shaped objects are copies of the same galaxy because the shapes are similar.
The most luminous sources of X-rays in the Universe - quasars and galaxy clusters - are powered primarily by gravity. These will be amongst the prime targets for observations with XMM.
Here we will look at the way in which gravity is able to provide huge amounts of power, before looking at the sources themselves. Questions in blue can be clicked to reveal the answers, but to test your understanding and engage your brain, it is best to consider your own answer before clicking.
![]()
How does gravity power work?
Gravity is a very weak force compared to electrical forces. For example, the electrical repulsion between two protons is approximately 1036 times stronger than their gravitational attraction. Given this - why does gravity dominate the Universe on astronomical scales?
![]()
Gravitational force and weight
Newtons gravitational force law: F=GMm/r2 is a good approximation except in regions of extremely strong gravity. A body of mass m (normally measured in kilogrammes) at the surface of the Earth will be attracted towards the Earth's centre with a force given by this equation, where M is the mass of the Earth and r is its radius. This force is referred to as the weight of the body. It is not the same as its mass, it doesn't even have the same units. So, does a set of bathroom scales measure the mass or the weight of an object?
Since M and r are approximately the same over the Earth's surface (actually r varies by about 0.3% between the poles and the equator), weight (in Newtons) is just an almost constant factor times mass (in kg) throughout the surface of the Earth. It is therefore possible to mark scales in kg (or pounds etc.) rather than Newtons, and this is what is often done.
![]()
Orbits and weightlessness
A striking illustration of the difference between weight and mass is the behaviour of bodies in orbit. As everyone knows, an astronaut in an orbiting space capsule is "weightless". However, his mass (for example as it relates force and acceleration in F=ma) is unchanged. Most of the general public believe that this weightlessness is due to the fact that the astronauts are a long way from Earth, which is the source of the gravity. However, this cannot be correct. The altitude of a typical space shuttle orbit, for example, is approximately 500 km above the Earth's surface. Comparing this with the radius of the Earth, 6371 km, you can see that the value of r in the gravitational force equation, F=GMm/r2, is not that different in orbit. So, why are astronauts weightless?
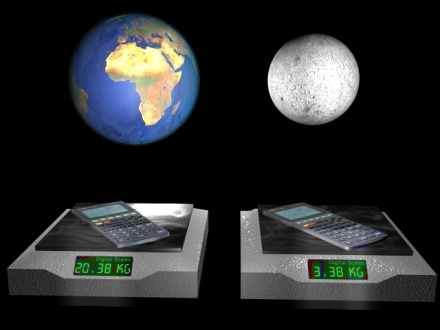
IMAGE - Identical objects have the same mass but a different weight
Scales are designed to be used on Earth. If a bathroom scale was taken up to the Moon and a mass was measured, it would say the mass was less (physically impossible)! However, scales really measure the weight of an object and this relies on the magnitude of the gravitational force. Therefore, when an object's weight is measured on the Moon, it would be less since the gravitational force is 0.155 of what it is on Earth
![]()
Gravitational potential energy
A great deal of energy is required to get a rocket into orbit. Some of this energy is converted into gravitational potential energy. Conversely, when a body falls onto the Earth's surface from space, the gravitational force accelerates it, turning its gravitational potential energy into kinetic energy. The gravitational potential energy of a body of mass m, at a distance r from the centre of a mass M is U=-GMm/r, and the potential energy of a unit mass, V=-GM/r, is referred to simply as the gravitational potential. The minus sign in this equation is important, since the gravitational potential must obviously be higher for a body at a greater height above the Earth's surface. Notice that V is defined so that it reaches a maximum value of zero when the body is infinitely far away from the source of the gravity.
So, how fast would a body be moving if it fell to Earth from a very large height, and how much energy would a 1 kg weight release on impact (N.B. The mass of the Earth is 6.0x1024 kg, and its radius 6,371 km.)
![]()
Accretion power and X-rays
As we have just seen, a large amount of energy is released when a body falls to the Earth from a great height. However, since V=-GM/r, even more energy would be released if the Earth were denser, so that its mass was squeezed within a smaller radius. The ultimate in high density (short of a black hole) is achieved in astronomy in neutron stars, which are produced in supernova explosions which end the lives of massive stars. A neutron star has a mass similar to our sun (2.0x1030 kg - i.e. over 300,000 times greater than the Earth) compressed into a sphere with radius of only about 10 km. One cubic centimetre of neutron star has a mass of over 400 million tonnes! The gravitational potential on the surface of such a star is approximately 1016 J kg-1, so that a kilogramme dropping onto the surface would release an energy equivalent to a 2 megatonne nuclear bomb (about 100 times more powerful than the bomb dropped on Hiroshima).

IMAGE - A diagram indicating the extreme density of neutron star material
Because a neutron star is so dense ,one pinhead would weigh about the same as two large battleships!!
When such a neutron star occurs in a close binary system, it may capture gas from its companion. As this falls onto neutron star surface (it actually goes into orbit first, forming a disc) it is heated to very high temperatures. Such X-ray binaries are the brightest sources of X-rays in our galaxy, with luminosities of up to 1031 W.
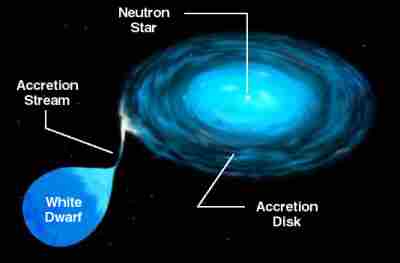
A binary system in which a neutron star accretes material pulled from a companion star. The gas spirals down onto the neutron star surface through a disc. Both the disc and the neutron star surface get very hot (107 K or so) due to the large release of gravitational potential energy, and emit X-rays. Courtesy of NASA
![]()
Escape velocity and black holes
We have seen that a body falling to Earth from infinity hits the surface with a velocity of about 11 km s-1. Conversely, if you could throw an object upward with a velocity of 11 km s-1, it would have enough energy to escape from the Earth altogether, and travel off to infinity. In the case of a neutron star, a simple calculation shows that the escape velocity is about 1.4x108 m s-1, which is about one half of the velocity of light!
Now light is affected by gravity (this is one of the results of Einstein's General Theory of Relativity). It is not decelerated in the same way as a moving body, but its path can be bent, and its frequency shifted. As light escapes from the surface of a neutron star, it is redshifted - so that its frequency drops, and its wavelength gets longer. If neutron stars were just a bit denser, then the escape velocity would equal the velocity of light, and radiation would be infinitely redshifted as it tries to escape (i.e. its frequency would drop to zero). It would be unable to escape! Such an object would be a black hole.
![]()
Gravitational lenses
According to Einstein's theory of General Relativity, gravity can be thought of as a distortion of the fabric of space-time. One consequence of this is that light rays passing close to a body are actually bent slightly towards it. In the case of light rays passing close to a black hole, this bending can be very extreme, as shown in the picture below.

IMAGE - Image showing the bending of light near a black hole
As can be seen if you move your mouse over this picture, the light from the distant source can actually appear to the observer on Earth to arise from points above and below the black hole.The black hole acts very much like an optical lens, and this phenomenon is known as 'gravitational lensing'.
Please move mouse over image
So how would a star centred precisely behind the black hole appear to the observer?
A star which is not directly behind the black hole, would generally have its apparent position shifted away from the hole, due to the bending of light. If we could see a black hole against a background of stars, it would therefore look something like the artists impression below. The hole is not simply blocking the light from the stars behind, it is actually diverting it, so that they appear to have been pushed aside.
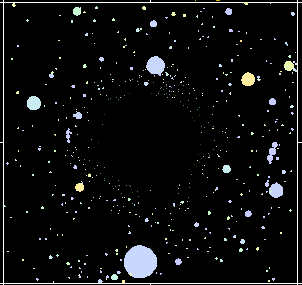
Computer generated image of the appearance of a black hole seen against a background of stars. The immensely strong gravitational force field close to the black hole bends the light coming from behind it, so that the apparent position of stars are shifted. (Picture credit: Robert Nemiroff, Michigan Technological University.)
Related links
More on forces
More on black holes

