LATENT HEAT - con'd
What is happening to cause the heat to become latent?
We can now see what is happening when we heat a substance as it is changing phase. The energy is going into making the matter further apart; that is to say the atoms are less well bound when they are further apart. Because energy is being expended in the process the atoms are not just being separated, they are being forced up some kind of a hill. In physical terms the energy is going into potential energy which can be recovered later.
So what does the "hill" look like?
We are not so much looking at a hill but more at a valley between two hills, or perhaps more realistically, like the moat around a hill castle. Such a moat is called a potential well.
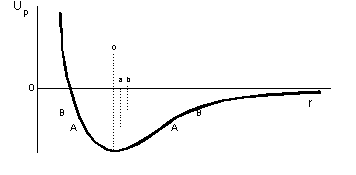
What is plotted here is the potential energy Up between two particles as a function of their separation r. It is the composite really of two curves; the part to the left represents a repulsive force (the magnitude of which is given by the gradient of the line) and the part to the right represents an attractive force. The curves taken together define a "well" which has a minimum in potential energy. The curve to the left typically has a greater slope than that on the right so the "well" is not symmetric about its minimum point.
The bottom of the well corresponds to the minimum energy so one of the particles, if free to move, will go to this position with respect to the other particle. Any movement in either direction is uphill so the particle returns to its stable position. Under these circumstances the particles are "bound" and the "binding energy" is the depth of the well in energy units below the horizontal axis. The deeper the well the more firmly bound are the two particles. The separation of the two particles in this situation is thus o.
Can the particle get out of the well?
At non-zero temperatures (on the absolute Kelvin temperature scale) the particles will have some motion and therefore some kinetic energy. So the bound particle will not sit at the bottom of the well but a little way up, say at the level A-A. Since the particle can occupy any position along A-A it can have any separation within the limits defined by the two ends of the line A-A. This is as if the two particles were bound by a piece of elastic. Their mean separation is now a which is greater than o.. Hence their separation has increased and they are less well bound than previously. If we raise the temperature a little bit further the system could be represented by the line B-B with a mean separation b, which in turn is greater than a., and the particles are even less well bound. If these particles were just a pair amongst a crystalline solid such as a metal, the whole system would have expanded as a result of the heating; that is thermal expansion.
If we were to raise the kinetic of the particles by an amount equal to the depth of the well the particles become unbound and the bond broken. This is what happens when for example we heat molecular hydrogen and dissociate it into two hydrogen atoms. The energy required for this is 7.0 x 10-19 J (or 4.4 eV) per molecule.
So we can see from this that energy is absorbed into potential energy when bonds are broken and the particles move further apart. Conversely potential energy is released as kinetic energy when the particles move closer together, bind and become more stable.
Does the latent heat phenomena occur at all phase transitions?
Yes. This follows from the discussions above since phase transitions are a manifestation of changes in the binding energy.
Can phase transitions be brought about by changes other than temperature?
What is essential is to effect a change in the inter-atomic separation such that the atoms can then re-arrange themselves. It does not matter too much how that change is effected. A more obvious mechanism than a change in temperature is in fact a change in pressure. By changing the pressure the atoms can be caused to be closer or further apart. Temperature and pressure in this sense act in opposition. The separation of atoms is decreased by increasing the pressure but can then be restored by increasing the temperature.
We can see this in the diagram below which characterises the transition between a gas and liquid.
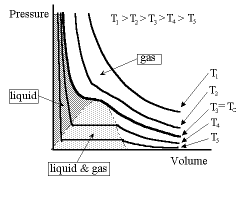
What each curve tells us is what happens to the pressure as we change the volume containing the gas, keeping the temperature of the gas fixed. We can visualise this system as being the volume contained by a piston which we can move in and out, though in so doing we must allow the system always to return to its constant temperature (i.e. isothermal expansion/contraction). Consider the curve marked T4 starting at the right-hand end. Here we have a gas. As we move to the left, pushing on the piston, the pressure rises and the volume decreases, that is, the atoms in the gas are getting closer to each other. We then get to situation whereby a further reduction in volume does not change the pressure; it is almost as if some of the gas atoms were simply disappearing from the volume. We then emerge from this phase and again the pressure increases with decreasing volume, but this time far more steeply than originally. What we have now is matter which is far less compressible than before. This is the liquid. What was happening in the transitional phase was that some of the atoms were not in fact disappearing but seemingly occupying a much smaller volume than they were previously and were not therefore as noticeable. Here the liquid and gas co-exist in the volume.
So an increase in pressure brings about a change of state from the gas to the liquid. We can recover the situation by increasing the temperature, i.e. by moving diagonally from bottom left to upper right.
For temperatures greater than T3 there is no "flat" transition region, that is, the atoms can be forced closer to each other but never close enough that they bind together to change their state into a liquid. This boundary temperature is called the critical temperature Tc.
Is Van der Waals equation to do with different particle separations?
Yes, it is. We can see this from the diagram we have just been discussing.
As we move to higher and higher temperatures the curves appear to have less distortion and begin to indicate the characteristic reciprocal relationship between the two parameters pressure and volume, P
1/V or more simply PV=constant. This is the ideal gas law which can be derived from kinetic theory provided it is assumed that (a) the atoms/molecules themselves occupy a negligible volume and (b) the atoms/molecules spend most of their time well separated. These actually amount to the same thing since, in the case (a) we have to ask "a volume negligible to what?". The answer is "compared to the volume containing the atoms and the spaces between the atoms". This is satisfied if the atoms are well separated, which is assumption (b). We can see that neither assumption is valid for small volumes.
Hence as the volume is decreased (a) is no longer a good assumption and so our effective volume has to be decreased by the amount occupied by the atoms/molecules. That is we should replace V by (V-b) where b is some small constant (volume). Also when the atoms are relatively close they experience the attractive force between them which we discussed earlier and which is equivalent to a sort of external pressure. Therefore P also has to be modified in a way which increases with volume decrease. Hence P can be replaced by (P+a/V2) where a is a constant and the equation now becomes
(P+a/V2). (V-b) = constant
or, in its more general form
(P+a/V2). (V-b) = RT
where R is the universal gas constant. This equation is known as van der Waals equation and describes the distortions in the graph above very accurately, that is it describes the behaviour of a gas close to its phase transition.
What conditions are required for other phase transitions?
It follows from the discussion above that the conditions for a phase transition are defined by temperature and pressure. For a given temperature less than the critical temperature there is a pressure at which a transition occurs, and similarly at a given pressure there will be a temperature for transition. The respective values will also depend on the substance. Hence there are combinations of temperature and pressure associated with each state of matter delineated by boundaries, a transition of which results in a phase change. For example, the curve below shows these combinations for water. X marks the boiling point for water at normal pressure.
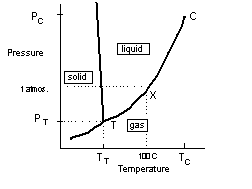
The critical temperature, TC, corresponds to the point C on the curve and is the temperature above which it is not possible for a gas to condense irrespective of the pressure (note the curve getting very steep at C). There is however another very significant point on this curve and this is the point, T. T is called the triple point and is the temperature/pressure at which all the phases, solid, liquid and gas are all in equilibrium with each other. Because of the uniqueness of this point, the triple point temperature, TT, is used as the standard for defining the absolute temperature scale.
We can see from this that for temperatures greater than TT a liquid cannot be compressed into a solid but at pressures less than PT a phase change between a gas and solid can be effected directly (without the intermediate liquid phase ) simply by a change in temperature. This is called sublimation.
And what about glasses and plasmas?
Glasses are very viscous (stiff) fluids and essentially have the same structure as a liquid. The atoms are not in any regular structure but are orientated randomly. Given enough time glasses will flow.
Plasmas are formed when atoms are ionised, that is when the electomagnetic bond between the negatively charged electron (or electrons) and the positively charged nucleus is broken and the electrons are separated from the ion it leaves behind. This ionisation energy is very similar to latent heat but the energies involved are very much greater.
Calculate how much energy is required to ionise 1 kg of the water radical OH (which, to a first approximation, has the same atomic weight as a water molecule). The ionisation potential of OH is 13.0 eV.
Click here for the answer.
