What are moments and torques con'd

     Let us now add in some more masses which are attached to each other to form a rigid bar and let's drill a hole at O and put a fixed pivot through the hole normal to the paper.

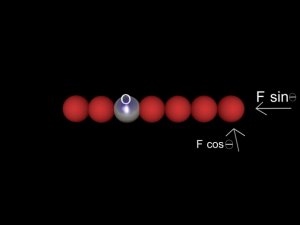
When a rigid bar is pivoted, the component of the force along the line of the bar has no effect, but the component perpendicular to the bar gives it angular momentum.

Please move mouse over image

     Application of the F sin 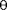force has no effect because linear motion is prevented by the pivot. Application of the F cos 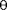causes the bar to rotate about O; again any linear motion does not occur because the bar is constrained by the pivot. Hence the bar acquires an angular velocity represented by a rate of change of 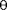with time, and angular momentum.

     The moment of the F cos force is defined as the magnitude of the force times the perpendicular distance from its line of application to the pivot point

moment = xF cos

     But x cos 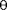= d

     Hence,

moment = Fd

     The product Fd is also called the torque and we see from this that its application results in a change in angular momentum of the rotating system.

     The torque is the rotational equivalent of a force in that in a linear system the force imparts momentum and is defined as the rate of change of momentum whereas in a rotating system the torque determines the rate of change of angular momentum.

     The unit of torque is the Newton metre, and although it has the same dimensions as energy it should not be confused with energy.

     It is relatively easy to visualise a torque and its effect when applied to a rigid body such as a bar. A good example of this is the spanner or indeed the torque wrench. The torque wrench is a calibrated spanner which acts as a rigid system until the required torque is reached and then the system "breaks" so that no additional force can be applied. Torque wrenches, spanners and screwdrivers are used all the time in the assembly of spacecraft where it is important to tighten up fasteners without the risk of overstressing them.

     It is not quite so easy to visualise torques in the sense of non-rigid systems such as a planet going round a star or an electron going round a nucleus, but it is equally applicable. Angular momentum exist in these systems just as readily as they do in rigid systems and changes in angular momentum can only be achieved through the application of a torque.