What then is angular momentum?

     It is easy to see that a mass moving in a non-linear way has angular momentum because it has an angular velocity. However, it would be wrong to infer from this discussion that a mass moving in a straight line does not have any angular momentum. Consider the bar that was described above and let it be stationary. If we fired a bullet at it such that the bullet hit the bar at any point other than the pivot point, the bar would rotate thus demonstrating that it had gained angular momentum. Where did that angular momentum come from (since angular momentum is a quantity which is conserved (see later))? It must have come from the bullet. If we were to shift the bar across such that that same bullet were to strike the bar at its pivot, then the bar does not rotate so the bullet cannot have had any angular momentum. So it would appear that this bullet has angular momentum in one case but not in the other. Which is right? The answer is that they are both right; it depends on how we actually view the situation; that is to say our frame of reference.

     Similarly when a stone is released from a rotating sling such as David used against Goliath, angular momentum is lost from the sling. But the stone, when released, travels in a straight line. Again where has the angular momentum lost by the sling gone? Answer, it is carried away by the stone (and slings only work if the stone is released from a point which is not the point about which it is being rotated).

     So a linear motion can possess angular momentum provided it is referenced to a point removed from the line of the motion. Angular momentum is defined as the linear momentum a body has times the perpendicular distance between the line of instantaneous linear motion and the point about which the angular motion is derived.

     Thus angular momentum is mvr. Although it contains the term mv, angular momentum is quite independent of linear momentum.

     These ideas are rather subtle but it is certainly worthwhile giving them a bit of thought.

If torques and angular momentum are the analogue of forces and linear momentum, what are the corresponding formulae and equations?

What is a couple?

     Returning to our example of the bar and simplifying the system by replacing F cos by F, let us now apply another force of equal magnitude F on the other side of the pivot in the opposite direction and at a distance y from the initial force.

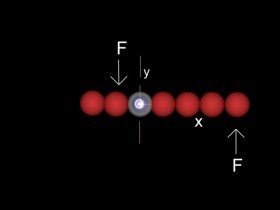
Whan a force is applied perpendicular to the bar on either side of the pivot point, the total torque experienced by the bar is just the sum of the two individual torques.

Please move mouse over image

     There are now two torques working in the same rotational sense giving a total torque of

Fy + Fx = F.(x+y)

     Let us now displace both forces by a distance z to the left.

     The total torque is now

F.(y+z) + F.(x-z) = F.(x+y)

We see that the total torque is unchanged; indeed it is independent of how the forces are applied provided that we do not change the distance between them.

     Setting (x+y) = l, the total torque is Fl. This is called the couple.

     A couple can only ever impart angular rotation provided that the forces are applied either side of the centre of mass (i.e. the balance point of the bar), and the rotation will not be about any arbitrary point but about the centre of mass.

     We could show this by putting a uniform bar (without any pivot through it) on a frictionless table. If we knocked it with a calibrated hammer at its centre we would get translational motion but no rotation. If we knocked it at any other point we would get translational and rotational motion. If we knocked it simultaneously in two places either side of the centre with identical knocks we would get rotation only, and this about its centre of mass. The relative magnitude of the angular velocity imparted in the various cases would simply depend on the position along the bar where it was knocked.