


![]() What is happening on the atomic scale??
What is happening on the atomic scale??
![]()
Knowing that solids exist at all tells us something about the forces that bind them. Clearly there is an attractive force involved otherwise such conglomerations of atoms could not form. But because such solids do not have the same density as pure nuclear matter tells us that there is a force keeping the particles from merging into one another. The fact that the situation is stable tells us that these forces are in balance. So, at long range the forces are attractive and at short range they are repulsive. In fact we know that it is the interplay of the electrons surrounding the nucleus in the atom that is responsible for the formation of these so called chemical bonds between atoms.

The overlap of the electron shells give rise to atomic bonds.
Since we are talking about stability it is helpful to use the notion of potential energy simply because a situation of stability is a situation of lowest energy. This can be described by a potential energy curve in which potential energy (U) is plotted against separation between the atoms (r). (See also latent heat.)
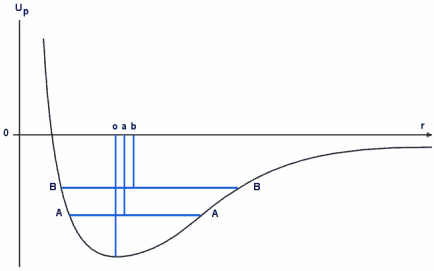
The potential energy curve,analagous to a simple gravitational well
As an analogy we can visualise such a curve as a simple gravitational well. A ball, having mass, falls down the slope on the right loosing potential energy and gaining speed (kinetic energy) until it meets the hill on the left. When its kinetic energy is eventually dissipated through friction the ball comes to rest at the bottom of the well and is in a position of stable equilibrium (a move in either direction encounters a force which returns it to its original position).

The potential well
Please place your mouse cursor over the image
In the case of two bound atoms we say that their combined potential is at a minimum when they are a distance of 'o' apart. This, if you like, is their natural separation when they are bound.
The magnitude, or the strength, of the forces is depicted by the slope of the potential energy curve. Hence, in order for us to have a representation of forces, the magnitudes of which locally increase with distance from the minimum, we need curves for which the slopes increase; i.e. a dish like shape (parabolic).
Initially we are only interested in what is happening right at the bottom of the curve and, to all extents and purposes, we can assume that the curve is symmetric about its minimum point; that is to say at some distance from the minimum point the forces differ only in their direction, not in their magnitude.
This can be seen if we plot the magnitude of the slope against r (in fact we have to plot , the negative of the slope, just to ensure that things "fall downhill" rather than uphill)
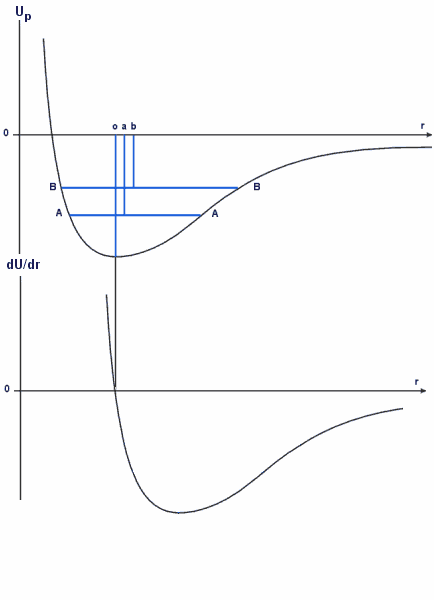
The second graph represents the gradient of the first. At 'o', the gradient reverses sign and is therefore a turning point. This is the minimum of the potential well.
A graph
The portion between the dotted lines m and n is linear and crosses the r axis at the point o. At this point the net force is zero and is the resultant of the two forces acting in opposite directions. The point o is the natural separation of the atoms.
How can the atomic bonds be represented?
Since the atoms are not absolutely rigidly held in place we can envisage the bonds as having some degree of elasticity. However when the separation is reduced from the equilibrium the bond acts under compression and when the separation is increased it acts under tension. Hence we could envisage the bond as acting as a spring the natural length of which is equivalent to the natural separation between the atoms. We can therefore picture a solid as an array of hard spheres all connected to their immediate neighbours by springs.
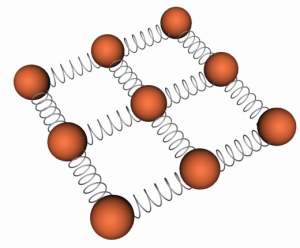
An atomic lattice can be represented by a series of spheres connected by springs.
What are the properties of a spring?
A spring can be made by taking some stiff wire and deforming it by bending it round a cylindrical former so that it adopts the permanent shape of a spring. The greater the number of coils it has the more spring-like it behaves. What we mean by spring-like is that if we apply a force along the longitudinal axis of the spring to either compress it or extend it and then remove the applied force, the force that is built in to the spring by so doing restores the spring to its original shape. Some springs are not particularly stiff such as the small springs that can be found in old fashioned watches, and some springs are extremely stiff such as those that can be seen supporting railway carriages. We talk of soft and hard springs though this is not to say necessarily that the metal from which they are made is necessarily soft or hard.

if a spring is slightly perturbed by a force (eg by suspending a mass), it will revert back to its original shape when the mass is taken off. Also, the spring will undergo simple harmonic motion.
Please place your mouse cursor over the image
If we were to be rather more exact in describing the properties of the spring we could draw a graph showing how the spring changes its length under the action of an applied force. Such a curve might look like
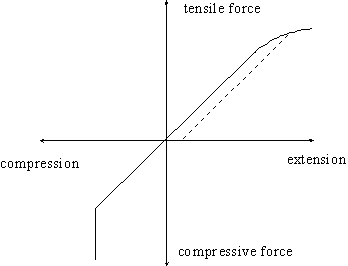
A graph
The vertical portion of the line (lower left) represents the situation where the coils are in contact. The curved portion (upper right) indicates that the coils have been separated so far that they have become permanently distorted so that, when the tensile force is then removed, the spring relaxes along the dotted line resulting in a spring which is now longer than it was originally. In passing, we should note that if we compress a spring, particularly one in which the length to coil diameter is large, we might never reach the vertical part of the curve. Instead, the coil goes all wobbly, and the coils loose their coaxial alignment. The spring has "buckled"; something it can never do under tension.

Springs with large radii will buckle if they are compressed too much
The linear part of the curve is the "working region" of the spring where its extension is proportional to the applied force. This is described by Hooke's law. The proportionality constant, k, is called the spring constant or spring stiffness, and is a measure of the gradient of the line in this linear portion. Hence the line is steeper for a hard spring than it is for a soft spring. Hook's Law in full is therefore
F=kx
When a spring is compressed or elongated, energy is stored in the spring and can be retrieved when the spring relaxes to its un-deformed state. The energy stored is
(1/2)kx2
The stiffness of the spring depends on a number of factors such as the length of the spring, the cross sectional area of the material, the diameter of the coils and the number of coils per unit length. It also depends on the properties of the material itself. A spring of given dimensions made of a "hard" material will be harder than a similar spring made of a "soft" material.
We can see that stiffness and hardness therefore mean similar things.

