


THERMAL DESIGN
If the Earth were surrounded by suns the same as our own Sun (which has a surface temperature of 6000K) what would be the temperature of the Earth?
![]()
ANSWER
It would be like being in an oven at 6000K so the Earth would be at 6000K.
But we are not surrounded by suns and so the temperature of the Earth will be less than 6000K. But how much less? This depends on how lossy is our oven. We can determine this by calculating what fraction of the "surface area" of the sky is occupied by the Sun.
![]()
ANSWER
Imagine the Earth to be at the center of a sphere such that the Sun forms part of the surface of that sphere. The sphere thus has a radius which is equal to the Earth-Sun distance (the astronomical unit). Let this distance be d and let the radius of the Sun be R¤ the fraction of sky covered by the Sun
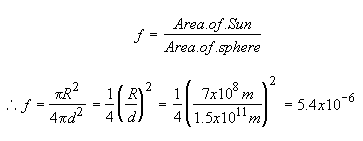
That is to say it would take 1/f Suns to completely cover the sky and this is about 200,000 Suns
See if you can use this number to obtain the temperature of the Earth by scaling the Sun's temperature.
We could assume that it scales linearly i.e. TE = f x T¤
Thus TE = 5.4x10-6 x 6000 = 0.03K
This is rather cool so cannot be correct. What is wrong?
The power (rate of transfer of heat) emitted by a surface at temperature T goes as T4
(This is Stefan's Law P=![]() AT4 where A is the surface area and
AT4 where A is the surface area and ![]() AT4 = 5.7x10-8 and is called Stefan's constant)
AT4 = 5.7x10-8 and is called Stefan's constant)
So we need to scale as T4 i.e. TE4 = f x T¤4 or TE = (f)0.25 x T¤
So TE = 289 K (or 17oC)
But the Earth's albedo is 0.39. That is to say it reflects about 40% of the incident sunlight which leaves only 60% for heating up the Earth.
So TE4 = 0.6 x f x T¤4
Therefore TE = 254 K (~ -20oC)
This is actually the temperature close to the top of the atmosphere at about 10 km where in atmospheric terms we are close to space.
Click here to return
![]()
STEFAN'S LAW
Let us say that we need to achieve a detector temperature of less than 100K and that we only have enough room to have a cooling radiator of 0.5 m2. The detector dissipates 1W and we estimate that the parasitic heat load from the warm surround will be about 9W.
If we opt for a single radiator (0.5 m2) to radiate the total power of 10W we can apply Stefan's law P=![]() AT4 to show that, for a perfectly radiating surface, the temperature we can achieve is 136K. This does not meet the requirement.
AT4 to show that, for a perfectly radiating surface, the temperature we can achieve is 136K. This does not meet the requirement.
If we have a 2-stage radiator where the 1st stage intercepts and radiates away the parasitic 9W and the 2nd stage radiates away the dissipative load of the detector, then we use Stefan's law twice for each radiator.
If we split the area 50:50 then we can show that
T1 = 159K and T2 = 92K
Thus achieving our objective.
If we split the area 10:90 then we achieve something apparently better i.e.
T1 = 237K and T2 = 79K
Clearly this is not the whole story because we have ignored the heat transfer between the shrouds which do the intercepting and which are coupled to the radiators. The magnitude of the transfer will be greater in the second case because there is a temperature difference of 158K driving it compared to that of 67K in the first case. So there is a limit to which we can divide up the area. It can be shown that there is an optimum solution and this confirms the common sense approach that if we have an n-stage radiator the dedicated areas should progressively increase from the outer radiator to the inner.
Click here to return to XMM Satellite Schoolpage
![]()
MECHANISMS
Think of a goods train comprising a number of trucks which are fairly loosely coupled. Energy can be transported from one end of the train to the other by the trucks bumping into one another i.e a series of collisions.
This is the kind of mechanism by which heat is transported by conduction and radiation. In the case of conduction the trucks are particles (atoms, electrons etc) and the energy is the kinetic energy of the particles.
In the case of radiation things are slightly more complicated in that the 'particles' here are the photons (packets of energy-carrying, electromagnetic radiation). But photons do not interact with photons, only matter. So what happens is that the a photon is absorbed by an atom which then re-radiates another photon which is then absorbed and re-radiated again and again. In both the above cases energy is passed from one agent to the other via collisions. Indeed the theory for the mechanisms of conduction and radiation are very similar.
Convection is the bodily motion of the agent.
Conduction and radiation always occurs to some extent or other. Convection only occurs under specific conditions.
In the Earth's atmosphere all three mechanisms are operative. The warm earth radiates infrared radiation which is absorbed by the atmospheric molecules quite close to the ground and then re-emmited onwards. Air also conducts energy (though not very well) and cold air in contact with a warm earth can heat up as a result of this contact. But we also know that cells (or pockets) of air move as a body (warm air rises and cold air sinks). We experience this sometimes when we fly through clouds and it can be quite dramatic; this is convection. In addition such pockets can be driven by winds (often the horizontal components of the convective circulation); this is how we get the meteorological warm fronts and cold fronts.
Similarly in the oceans, convective currents of water are very important in transporting heat (eg, the warm Gulf Stream)
Click here to return
![]()
TEMPERATURE
Temperature is a rather complicated concept. It is to do with how energy is distributed between a system of particles whether they be atoms or electrons or even photons (packets of electromagnetic radiation).
Consider the following thought experiment. You (in spirit only) are in a large empty room (even empty of all the air) which has rigid but perfectly elastic walls and in which there is no gravity. There is a small aperture in one of the walls through which are projected say 100,000 perfectly elastic, very small billiard balls, each with a velocity of 30 mph. You have a little hoop of wire through which the balls can pass and which measures there velocity. What happens when you take speed measurements with your hoop and construct a histogram showing the number of billiard balls with given speeds?
Click here to return
If you take measurements immediately the balls are still all likely to have the same speed of 30 mph. If you wait for a long time however you will find that most of them will have speeds of about 30 mph but some will be move more slowly and some move more quickly; that is they display a distribution of speeds (or energies). If you wait even longer and repeat your measurements you will find that nothing has changed; the system has settled down and has reached a state of equilibrium. This equilibrium has been reached because the balls have shared their energies through collisions with each other. We find that this equilibrium distribution is described by a mathematical function which only has one other variable (besides numbers of particles and speed) and this parameter is the temperature.
This distribution is called the Maxwell-Boltzmann distribution.
Photons cannot exchange energy directly with each but have to use matter as a "third party"; this could be the walls of the room for example. The photons too then come in to equilibrium and end up with a similar (though not identical) distribution of energies (we have to say energies here rather than speeds because all photons travel at the speed of light). This distribution is called the Planck distribution (or sometimes the blackbody radiation spectrum). Again this is specified by a single parameter, the temperature.
Click here to return
![]()
ELECTRICITY THROUGH A WIRE ANALOGY
We can draw parallels between these systems in the following approximate way.
Heat Electricity Fluid
Driving agent temperature voltage pressure
D difference difference difference
Resisting agent thermal electrical pipe/fluid
R impedance resistance resistance
Flow rate power (Watts) current (amps) flow (litres/sec)
F (energy/sec) (charge/sec) (fluid vol/sec)
If we consider this flow to be constrained by say a solid cylinder, a wire, or a pipe respectively, then generally we can say that
R=C1 x A/l
Where A is cross sectional area, l is length and C1 is a constant of proportionality
And that D = C2 x FxR
Where C2 is another constant.
The obvious example of this is Ohm's Law for electricity which states that V=iR
Click here to return
![]()
TEMPERATURE OF THE EARTH
You have to think about what other factors affect the temperature of the Earth and the time scale on which they occur.
The Earth's orbit round the Sun is not circular but slightly elliptical. In January the Earth is at its closest point and therefore receives slightly more heat input than in July.
The Sun has a cyclic activity variability on a time scale of 11 years (the so-called Sunspot cycle). This has a small effect on the heat input and climate perturbations occur.
The properties of the Earth's "blanket" (its atmosphere) change as a result of man made emissions. These in turn affect the ozone layer which then influences the amount of radiation from the Sun reaching the Earth's surface. It would seem that the time scale of this is frighteningly short.
In the longer term there are the big climatic changes which we know as the ice ages.
Click here to return
![]()
NOISE
Consider the human ear. It is a detector (attached to the brain). If you are trying to listen to something and there is a lot of external background noise then you ca nnot hear someone who is trying to talk to you. If you have an illness called tinnitus then the brain is aware of a lot of internally generated noise and again it make s it less easy to hear when someone speaks. Both sources of noise contaminate the signal which we are interested in i.e. what the person talking to you has to say.
In the daytime we do not see stars, not because they are not in the sky, but their signals are being swamped by the contaminating solar radiation which is being scatter ed in the atmosphere.
All physical detectors have internal noise arising, for example, from their electronics. This can usually be reduced by cooling.

