


![]()
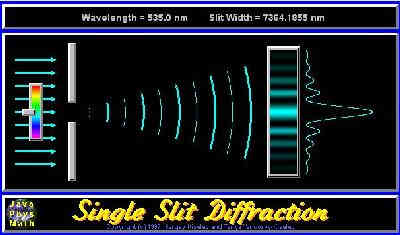
What happens to a light beam passing through a narrow aperture?
To resolve this problem light must be considered as a wave - not as a particle or photon. So the question could be re-phrased as: what happens when a wave that has to pass through a narrow aperture?
The preliminary step to understanding this problem was published in 1690 by a Dutch physicist Christiaan Huygens. The principle he described has since become known as Huygen's Principle. It states that:
"Every point on a wavefront serves as the source of spherical secondary wavelets, such that the primary wavefront at some later time is the envelope of these wavefronts. Moreover, the wavelets advance with a speed and frequency equal to those of the primary wave at each point in space."
So what does this mean? Recall that a wavefront is a surface over which a wave has a constant phase. Huygen's Principle states that every point on this wavefront is acting as an individual point light source, with its own set of secondary wavelets.
![]()
What does this mean for a source of parallel waves arriving at an aperture?
If you want to see what happens as the wavelength of light changes click here
This shows that the light leaving an aperture is spread out. If the aperture is very small, about one wavelength across, the wave leaving the aperture will appear as a point source of light. This is Huygen's Principle in action, as we are sampling just one of the secondary wavelets on the incident wave.
![]()
What happens if the aperture is slightly larger?
As the aperture size increases the number of secondary wavelets contributing to the diffraction pattern increases. Each of these wavelets will superimpose to form a diffraction pattern, as shown in the diagram above. If a very large aperture is illuminated a very large number of secondary wavelets will contribute to the outgoing wave, which will therefore be very nearly a parallel wavefront.
If a lens was used to focus this almost parallel light, an image of
bright and dark rings is formed. The central bright region, known as
the Airey's disk determines the resolution of the image. Consider an
image of two stars, if they are well separated the two Airey's discs
will not overlap, but if the separation is reduced a point is reached
where they do overlap. The limiting resolution is reached when the
overlap so much that they are indistinguishable from a single Airey
disc. This limiting resolution ![]() , which is known angular
resolution is determined by the diameter of the aperture d:
, which is known angular
resolution is determined by the diameter of the aperture d:
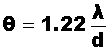
Where ![]() is the wavelength of light
illuminating the aperture.
is the wavelength of light
illuminating the aperture.
This simple formula shows us why a large telescope with a large diameter mirror will have a much better angular resolution than the naked eye.
![]()
What is the size of the aperture of a telescope?
The aperture size of a refracting telescope is typically the size of first lens the light from a star encounters. This lens can be visualized to be like the aperture considered above. A reflecting telescope isn't so obvious. In this case we have to think of the primary mirror as the aperture, but this time instead of transmitting the light like aperture it is only reflecting a portion of the received light. So the aperture size of a reflecting telescope is the diameter of the primary mirror.
The angular resolution of the XMM mirrors would be calculated by considering the light reflected off each shell, in a similar way to a reflecting telescope. There would be an addition complication to this calculation though, as the mirror supports and the central aperture stop would have to be included. Taking all of these factors into account XMM is expected to have angular resolution of 15 arcseconds.

