Superposition of waves?

     Huygen's Principle could be used to understand how light behaves when passing through a single aperture. What happens if instead of a single aperture there are now have two narrow apertures with overlapping diffraction patterns.

     Consider the experiment shown below.

     Two narrow slits are illuminated by a light source of a single wavelength, and the resultant light is projected onto a screen some distance away.

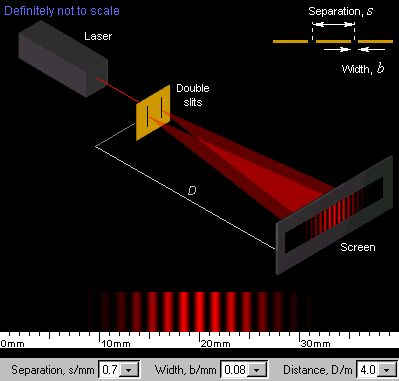
Image taken from MATTER web site.

     Click here to see an interactive version of this diagram which allows you to change the experimental setup to watch what happens.

     The light emanating from the two apertures will appear as two point sources separated by a small distance. Thus the resultant amplitude pattern will be formed from the superposition of the two wave patterns. The rule for calculating the resultant from the two waves is that the amplitudes from the two wave patterns, A and B, will add together other, so that the resultant amplitude C observed is given by:

     A + B = C for every point in space.

     The measured amplitude therefore will depend on the phase of the two waves at the point you are measuring.

Bright Regions

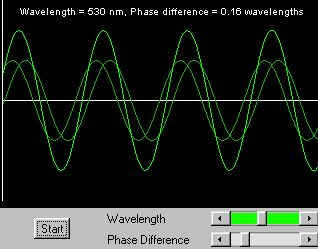
     Two nearly in phase waves.

     The waves from the two diffraction patterns are in phase in the bright regions, thus the two amplitudes add up.

Dark Regions

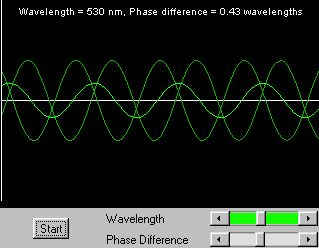
Two nearly out of phase waves.

     The waves in the dark regions are out of phase, so the total amplitudes subtract

     The two images above are from the MATTER web site

     Click here to see an interactive version which allows you to change the phase difference and wavelength of the two waves at the MATTER web site.

Young's Double Slit Experiment

     Young first performed the double slit experiment shown above in 1802. It showed clearly for the first time the wave nature of light as there is no way of predicting the diffraction pattern seen by considering light as particles.

     Thus if we have two overlapping waves have the same frequency and amplitude, the resulting amplitude pattern will be determined by the superposition of these two waves. There will be regions of zero disturbance where the waves are out of phase and regions of enhanced disturbance where they are in phase.

     The direction of the region of the maximum light intensity can be predicted by considering how far the light must travel for the waves to be in phase. The path difference between the two path lengths must be an integer number of wavelengths for constructive interference. Thus for the light interfere constructively the path length difference L must be given by:

     Where m is and integer and is the wavelength of the light

     This wavelength dependence shows that different wavelengths of light will produce different diffraction patterns. A coarse spectrometer could be produced using this dependence. A much better spectrometer in produced when a large number of regularly spaced apertures are used. This is known as a diffraction grating.