


The double slit experiment, first performed by Young in 1802, shows that when two diffraction patterns overlap the resultant disturbance is the sum of the amplitudes two original waves. What happens if there are now a large number of equally spaced apertures rather than just two?
![]()
In this case the waves originating from all of the apertures must be in phase to give the maximum intensity. This limits severely the number of points at which there is a maximum in amplitude. The only directions in which there would be a maximum in amplitude are when the path difference between the secondary wavelets formed by two adjacent apertures are multiple of one wavelength.
This can be represented mathematically as:
![]()
Where a is the separation of the grating apertures, ![]() is the angle at which the wavelets interfere positively, m is an integer, and
is the angle at which the wavelets interfere positively, m is an integer, and ![]() is the wavelength of light.
is the wavelength of light.
![]()
How would you use a diffraction grating?
Consider the experiment shown below. A diffraction grating made up of a large number of equally spaced slits is illuminated by a single wavelength of light. The resultant light pattern is projected onto a screen, and scanned with a microscope.
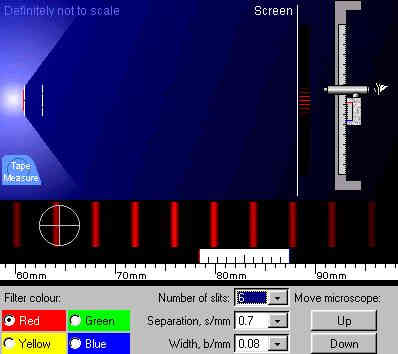
Image - taken from the MATTER web site. Click here to see an interactive version that allows you to change the experimental setup and watch what happens.
Each of the bright bars is where the light is in phase. The use of a microscope shows that these bars are very narrow, so the light is in phase over a very narrow range of angles.
![]()
How is a spectrum formed by a diffraction grating?
The central bar corresponds to the case m=0, and the light is undeviated, q >=0. Thus and image of the illuminating slit will be formed. If m>0 the maximum intensity of light will be shifted away from the angle of incidence of the incoming light. This angle will be dependent on wavelength, see the grating equation above.
If the grating is illuminated with a wide range of wavelengths of light, eg star light. Then each wavelength will be deviated by a slightly different angle. Therefore the light on our screen will appear to be spread out in wavelength. Thus a spectrum of the incident light will be formed. When m=1 the resulting spectrum is known as the 1st order spectrum, 2nd order for m=2, and so on.

